Punto de inflexion

La recta normal

Punto critico maximo

Puntos criticos : Maximos o minimos

Punto critico minimo

La recta normal-Punto critico Maximo o Minimo

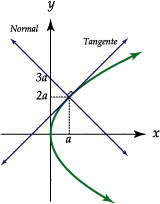
Recta normal
La recta normal es una curva en un punto de tangencia dado, es una recta perpendicular a la tangente de dicho punto.

Para determinar la ecuación de la recta normal a una curva de una función (x) en un punto (x, y) utilizamos la ecuación:
m= (-)1 /f´(x)

Caso #1
Determinar la ecuación de la recta normal a la curva en el valor “x”, en el punto dado para cada función.
y= x2 +7 en x=1

Paso 1. y= (1) 2 + 7
y= 1 + 7
y= 8

Paso 2. m= - 1/2x

m= - 1/ 2

m= - 0.5
Paso 3. y- y1= m(x- x1)
y- 8= -0.5(x- 1)
y= 0.5 + 8.5








Puntos Críticos: Máximos o Mínimos
El punto crítico se ubica en el punto tangencial de una recta horizontal, la cual tiene pendiente igual a “0”. En una parábola de una función cuadrática el punto crítico se ubica en el vértice.


Para determinar la coordenada del punto critico, es necesario:
1. Resolver la primera derivada de la función
F(x)= x2 -4x +5
F´(x)=2x- 4

2. Igualar a “0”
2x-4=0
2x=4
x=4/2
x=2
3. Sustituir el valor de “x” en la función original.
F(x)= x2 -4x +5
F (2)= (2) 2 -4(2) + 5
y=4 –8 +5
y= 1 punto critico (2,1)


Caso #1
Localiza el punto critico de la función f(x)= x2 -4x -5
a b c
a>”0” hacia arriba
a<”0” hacia abajo
• Punto critico mínimo
*F(x)= x2 -4x -5
F´(x)=2x -4
**2x-4=0
2x=4
x=4/2
x=2
***F (2)= x2 -4x -5
F (2)=2(2) -4(2) -5
y= 4 -8-5
y=-9 punto critico (2,-9)

La Derivada

“UANL”
Preparatoria No.25
“Dr.Aguirre Pequeño”

“Definición de
Derivada”

La derivada es el limite del cociente del incremento de la variable dependiente entre el incremento de la variable independiente, cuando este tiende a cero, lím ∆y
∆x→0 ∆x

Al proceso para encontrar la derivada se le llama: diferenciación.
La definición de la derivada en términos de límites se emplea para demostrar las reglas de diferenciación.
Reglas básicas

1. Para una constante “a”
Si f(x)=a, su derivada es f´(x)=0
Ejemplo: f(x)=16
f´(x)=0
2. Para la función identidad f(x)=x
Si f(x)=x, su derivada es f´(x)=1
Ejemplo: f(x)=x
f´(x)=1
3. Para una constante “a” por una variable “x”
Si f(x)=ax, su derivada es f´(x)=a
Ejemplo: f(x)=7x
f´(x)=7
4. Para una variable “x” elevada a una potencia “n”
Si f(x)=xⁿ, su derivada es f´(x)=nxⁿˉ¹
Ejemplo: f(x)=x³
f´(x)=3x²
5. Para una constante “a” por una variable “x”elevada a una potencia “n”
Si f(x)=axⁿ,su derivada es f´(x)= anxⁿˉ¹
Ejemplos: f(x)=4x²
f´(x)=8x
6. Para una suma de funciones
Si f(x)=u(x)+v(x), su derivada es f´(x)=u´(x)+v´(x)
Ejemplo: f(x)=3x²+4x
f´(x)=6x+4
Regla de la derivada del producto
Se aplica a funciones formadas por la multiplicación de polinomios y la formula a aplicar es:
f´(x)=u´v+uv´
Ejemplo:
f(x)= (2x³+3) (3x4-5)
u´=6x2 v´=12x³
f(x)= (6x2) (3x4-5)+(2x³+3)(12x³)
f(x)=18x6-30x2 +24x6 +36x³
f(x)=42x6 +36x³-30x2
Nota:
*Al multiplicar cada elemento los exponentes se suman.
*Al juntar términos semejantes los exponentes quedan igual.
Regla de la derivada del cociente
Esta regla se aplica a la división de polinomios f(x)=u/v
y se aplica la formula:
f´(x)=u´v-uv´
v2
Ejemplo:
f(x)=2x u´=2
x+2 v´=1
f´(x)=2(x+2) – 2x (1)
(x+2)2
f´(x)=2x+4-2x
(x+2)2
f´(x)= 4_
(x+2)2
Nota:
*El denominador no se modifica.
Regla de la derivada de la cadena
Este proceso se aplica a la función formada por un polinomio elevado a una potencia, en base a la formula:
f´(x)=n (u)n-1 (u´)
Ejemplo:
f(x)= (2x³+3)5-1 u´=6x2
f´(x)=5(2x³+3) 4 (6x2)
f´(x)=5(6x2) (2x³+3) 4f´(x)=30x2 (2x³+3 ) 4